Visualizing Multiple Data Distributions

One of the first steps when exploring data is to look at its distribution. For single distributions, or for comparing a small number, histograms are great. However, as the number of distributions to compare grows, histograms become less and less useful for visualizing data. Fortunately, there are some good alternatives.
In this post, I’ll look at a few different plot types I explored when comparing the distributions of crashes by day of the week. More information about the data can be found in the original post: SWITRS: On What Days Do People Crash?
The Jupyter notebook used to make these plots can be found here (rendered on Github).
Box Plots
Box Plots, or box-and-whisker plots, are one of the simpler ways of plotting a series of distributions. The edges of the box show the 1st and 3rd quartile while the line within the box shows the median (2nd quartile). The whiskers show the extent of the data, but their usage is not standardized. Sometimes they show the full extent of the data, sometimes some percentage of the inner-quartile range, and sometimes one standard deviation from the mean. If they do not show the full extent, the points not included in the whiskers are plotted individually.
Box plots quickly convey some essential statistics about the distributions and make no assumptions about the underlying data, which is both a strength and a weakness. Their simplicity can hide important information, and their non-standard whiskers can cause confusion if what they represent is not clearly stated.
These box plots show the distributions of the number of crashes per day in California by day of the week from 2001–2015. From the box plots it is easy to see that there are more crashes on Fridays and that the weekends have fewer crashes than the weekdays. Most of the outliers are on the high side, but we can’t tell anything about the actual shape of the distributions.
Strip Plots
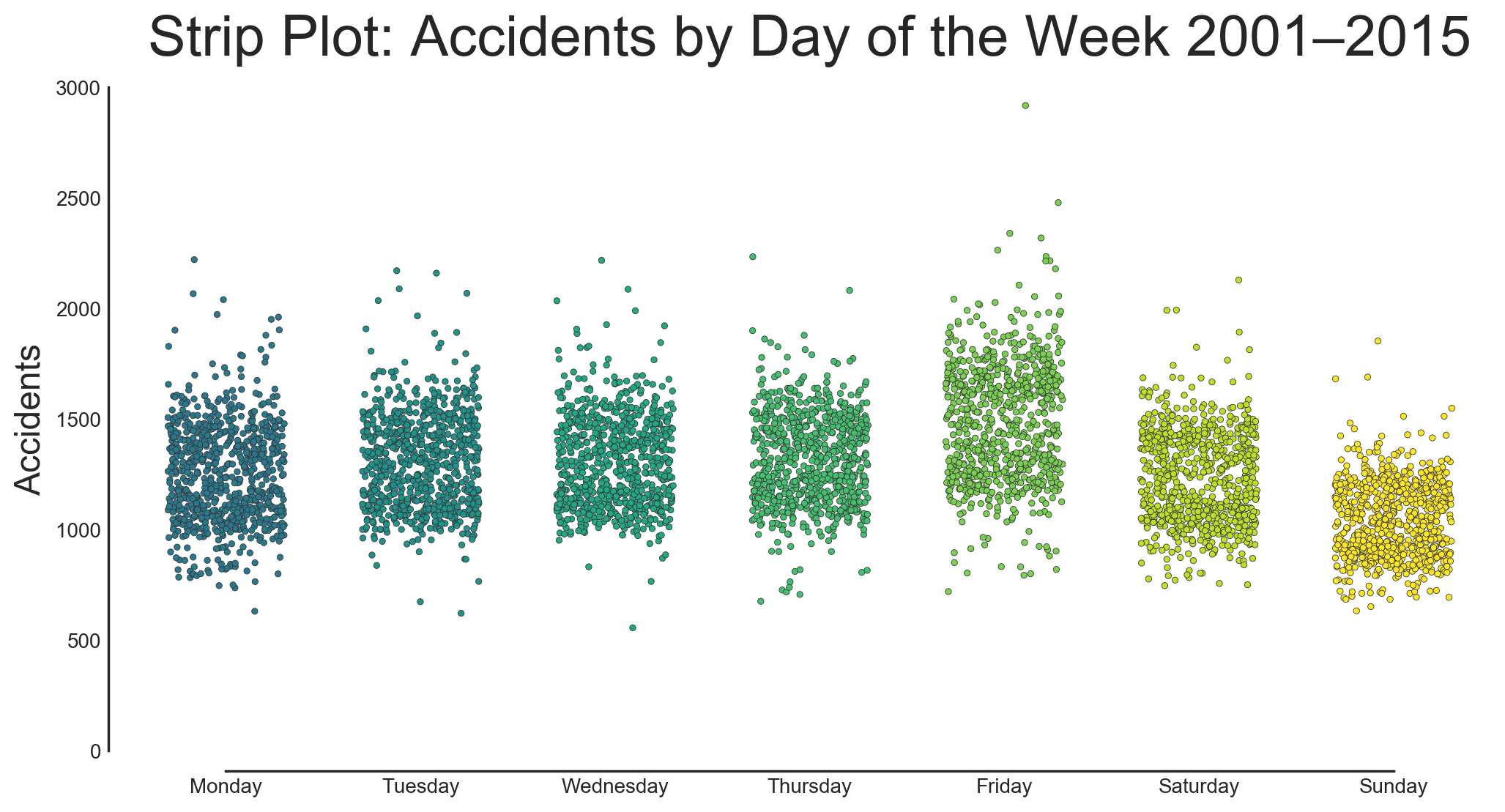
Strip Plots, also called dot plots or univariate dot plots, try to give us a little—well a lot—more information than box plots. They plot every point in the dataset, which can give you a good view of what is happening. They often have a bit of random jitter added to each point along the categorical axis so that the points do not overlap as much.
Strip plots make it is easy to see all the outliers. The density of points also gives an approximation of the underlying distribution, although this can be hard to judge by eye because the distance in the categorical axis, while meaningless, obscures the true distance between points. Overlapping points also make it tough to estimate the true distribution, especially as the number of points increases.
With the strip plot it is still possible to tell which days have more crashes, but without the quartiles to guide the eye it is not as easy. We can now start to see that the distributions are bimodal, although it is difficult to see details with all the points. Strip plots are enticing because they show literally all of the data, but plots which summarize the data are often more useful for large datasets.
Swarm Plots
Swarm Plots, also called beeswarm plots, are similar to strip plots in that they plot all of the data points. Unlike strip plots, swarm plots attempt to avoid obscuring points by calculating non-overlapping positions instead of adding random jitter. This sort of gives them appearance of a swarm of bees, or perhaps a honeycomb.
Swarm plots share many of the same advantages of strip plots, but without as much clutter to hide their salient features. Unfortunately, spreading out the points in a non-overlapping fashion limits the number of points that can be plotted—there is only so much space on the page! Additionally, the algorithm that calculates the positions is computationally expensive and so scales poorly as the number of points increases.1
This slow generation time is especially harmful during exploratory analyses. It is easy to keep engaged with the problem when a plot takes a second or two to pop up, but when they take more than a minute my productivity plummets as my iteration time explodes and I have to constantly context switch.
I generated this plot using a sampled subset of the data because the swarms piled up when trying to show the full dataset. Even so, you can see some of the points have piled up against the edges of each column. The swarm plot makes the relative crash rates easier to see than on the strip plot. The bimodal nature of the distributions is much clearer and their shape can almost be made out. However, the thickness of the plotted points causes the formation of the strands extending out from each swarm which make judging the true shape of the distributions difficult.
Violin Plots
Violin plots plots try to give an indication of the distribution of data without cluttering the plot by drawing all of the points. They do this by using kernel density estimation (KDE) to model the distribution. There is a lot of information to process in a violin plot so they can be a bit tough to read. The shape of the violin body indicates the number of observations: if the violin is thick at some value it means there are a lot of data points there, if it is thin then there are few. The inside of the violin is often marked to indicate additional information. The violins below have the quartiles draw inside them as dashed lines, but miniature box plots are another common inner marking.
The main disadvantage of violin plots is that the KDE bandwidth must be selected. Too low and the features of the data are washed out. Too high and the KDE overfits the data. This limits their usefulness when there are only a few data points. The lack of standardization when it comes to the inner markings also makes them hard to interpret if they aren’t explicitly explained.
The violin plots make the bimodal nature of the distributions crystal clear. Likewise it is easy to see that there is an increase on Friday and a decrease on Sunday. However, we have lost sight of our outliers. We can see that the Friday violin extends to almost 3000 crashes, but exactly how many data points go into that thin tail is unclear.
Conclusion
I like violin plots a whole lot! While swarm and strip plots show lots of detail and box plots provide good overviews with the summary statistics, I find violin plots to be a good middle ground. The KDE provides more detail than a pure box plot, includes the same useful summary statistics, and avoids cluttering the plot with every data point.
-
The box and violin plots in this post take about a second to render on my desktop. The strip plot take 5 seconds. The swarm plot take 74 seconds! ↩