Lab41 Reading Group: Deep Compression
This article originally appeared on Lab41's blog: Gab41. It is reposted here with permission.
The next paper from our reading group is by Song Han, Huizi Mao, and William J. Dally. It won the best paper award at ICLR 2016. It details three methods of compressing a neural network in order to reduce the size of the network on disk, improve performance, and decrease run time.
Pre-trained convolutional neural networks are too large for mobile devices: AlexNet is 240 MB and VGG-16 is over 552 MB. This seems small when compared to a music library or large video, but the difference is that the networks reside in memory when running. On mobile devices SRAM is scarce and DRAM is expensive to access in terms of energy used. For reference, the authors estimate that a 1 billion node network running at 20 FPS on your phone would draw nearly 13 Watts from just the DRAM access alone. If these networks are going to run on a mobile device (where they could, for example, automatically tag pictures as they are taken) they must be compressed in some manner. In this paper the authors apply three compression methods to the weights of various networks and measure the results. A diagram of the three methods and their results are below; I’ll walk you through them in more depth in the next few paragraphs.
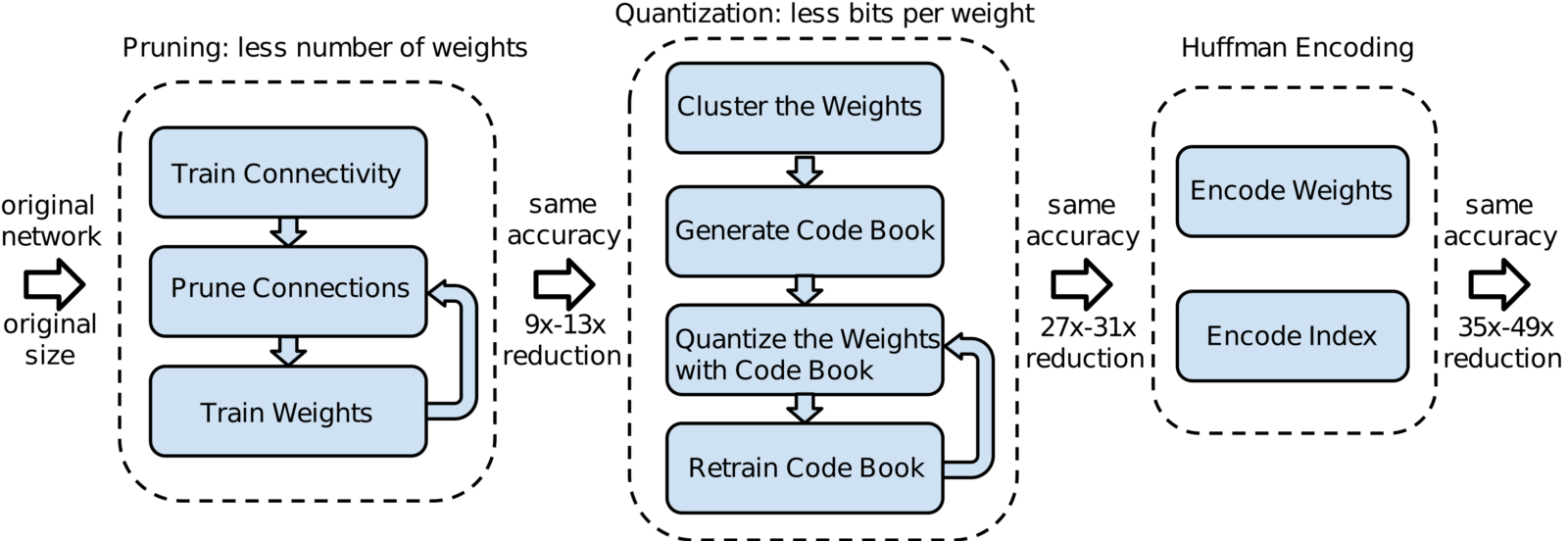
The first compression method is Network Pruning. In this method a network is fully trained and then any connections with a weight below a certain threshold are removed leaving a sparse network. The sparse network is then retrained to ensure the remaining connections are used optimally. This form of compression reduced the size of AlexNet by a factor of 9, and VGG-16 by a factor of 13. The authors also use a clever data structure that makes use of variably sized integers to store the network after this compression.
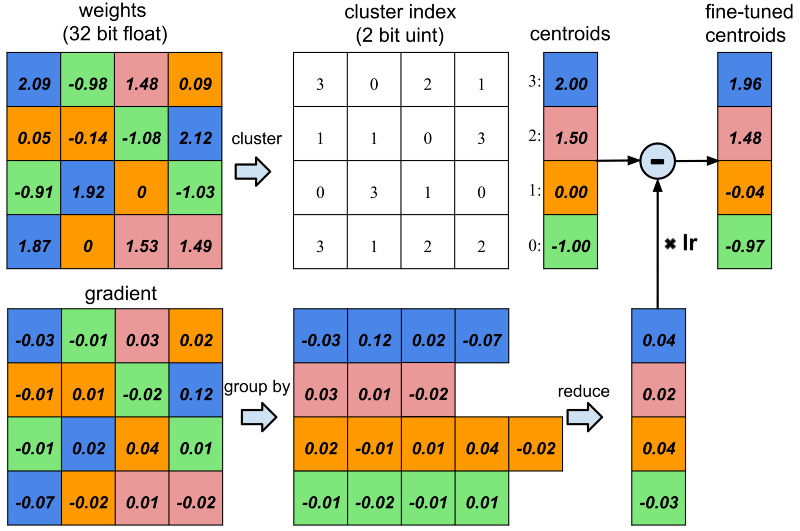
The second compression method is Trained Quantization and Weight Sharing. Here the weights in a network are clustered together with other weights of similar magnitude, and all these weights are then represented by a single shared value. The authors use k-means clustering to group weights for sharing. They explore multiple methods of setting the k centroids and find that a simple linear spacing of the centroids along the full distribution of weight values performs best. This compression method reduces the size of the networks by a factor of 3 or 4. A diagram with an example of this compression technique is shown below.
The third and final compression method is Huffman Coding. Huffman coding is a standard lossless compression technique. The general idea is that it uses fewer bits to represent data that appears frequently and more bits to represent data that appears infrequently. For more details see the Wikipedia Article. Huffman coding reduces network size by 20% to 30%.
Using all three compression methods leads to a compression factor of 35 times for AlexNet, and 49 times for VGG-16! This reduces AlexNet to 6.9 MB, and VGG-16 to under 11.3 MB! Unsurprisingly it is the fully connected layers that are the largest (90% of the model size), but they also compress the best (96% of weights pruned in VGG-16). The new, smaller convolutional layers run faster than their old versions (4 times faster on mobile GPU) and use less energy (4 times less). These results are achieved with no loss in performance! A plot showing the energy efficiency and speedups due to compression are shown below:
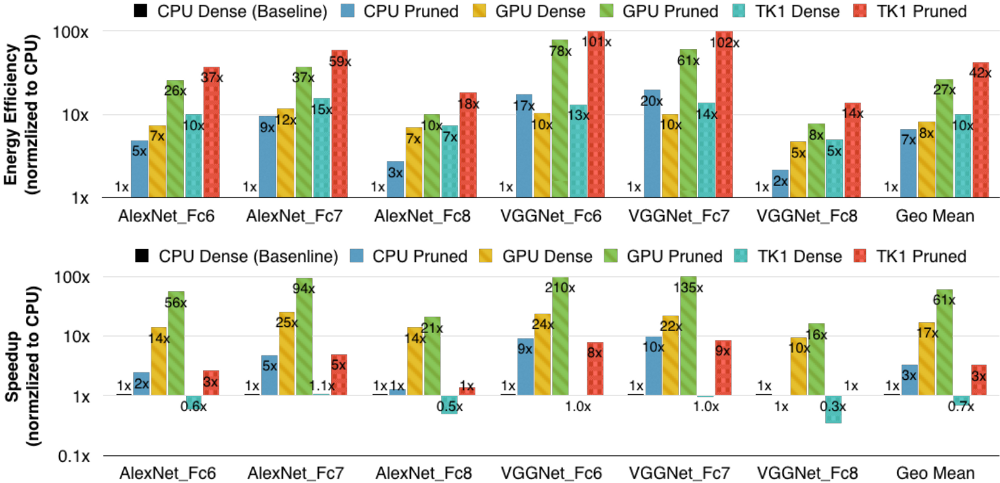
Han, Mao, and Dally’s compression techniques achieve an almost perfect result: the in memory size of a network is reduced, the run speed is increased, and the energy used to perform the calculation is decreased. Although designed with mobile in mind, their compression is so successful I would not be surprised to see it widely supported by the various deep learning frameworks in the near future.